P2P网络-KAD路由算法
以太坊源码之 KAD路由算法(二)
死磕以太坊源码分析之Kademlia算法
以太坊源码(01)：P2P网络及节点发现机制
Kademlia在2002年由美国纽约大学的PetarP.Manmounkov和DavidMazieres提出，是一种分布式散列表(DHT)技术，以异或运算为距离度量基础，已经在BitTorrent、BitComet、Emule、eDonkey、I2P暗网等软件中应用。
算法中每次消息交换都能够传递或强化有效信息，系统利用这些信息进行并发的异步查询，可以容忍节点故障，且故障不会导致用户超时。
KAD算法所要处理的问题：如何分配存储内容到各个节点，且如何新增/删除；如何知道存储文件的节点/地址/路径。
基础概念
1. 最短距离
P2P网络中为了避免通过泛洪方式查询数据，可以先定位到离存储数据的key最近的节点（键值对数据<key value>存储在和key逻辑距离最近的节点上），然后从该节点提取数据。
逻辑距离：d(x,y)=x⊕y，即异或距离。
将P2P网络中所有节点的nodeId与key计算逻辑距离，其中最小的便是最短距离。
例如key=101，则与节点100距离为1，与节点010距离为7。
2. 逻辑拓扑结构
P2P网络中每个节点都保存了其他节点的信息，节点查询数据时，需要去找到离数据key最近的其他节点，而如何快速高效地找到这个节点，就是逻辑拓扑结构要解决的问题。
假设节点nodeId是3位，网络中就有8个节点，将节点构造成一颗二叉树，所有叶子节点便是服务器节点。
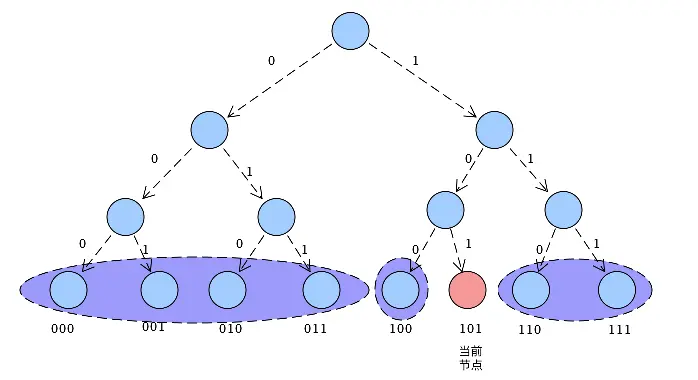
为了快速定位其他节点，采用分层规则：从最低位开始，在第一次出现不同位时，划到同一层。
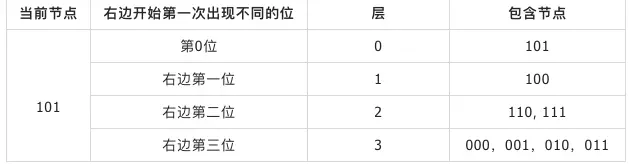
另一种分层解释思路：对于这颗二叉树上的任意一个节点，都可以将树分解成一系列连续的、不包含自己的子树。树自顶向下，最高层由二叉树在去掉根节点后不包含自己的另一颗子树的叶子节点构成，逐层以此类推，直到分割完整颗树。
根据分层规则，层数越高距离越远，第i层的距离范围为[2i-1, 2i)。
在查询数据时，用key与当前节点nodeId计算距离，从距离所在层中找节点去查询数据，而不用泛洪查找。
3. K桶
以太坊中节点ID远不止三位，随位数（层数）增加，各层对应的节点就越来越多。
为此提出K桶（K-Bucket）概念，每层只记录K个节点（K为系统级常量）。理论上只要知道某一层的一个节点就能够遍历整层的所有节点。K不取1，是由于分布式下节点动态变化，可能宕机。为平衡系统性能和网络负载，需要调整K值大小，但必须是偶数，如BT的K=8，以太坊K=16。
每层中存储的节点根据与当前节点的距离，由近及远排序。（个人理解：这里的排序用于查找数据时的快速定位）
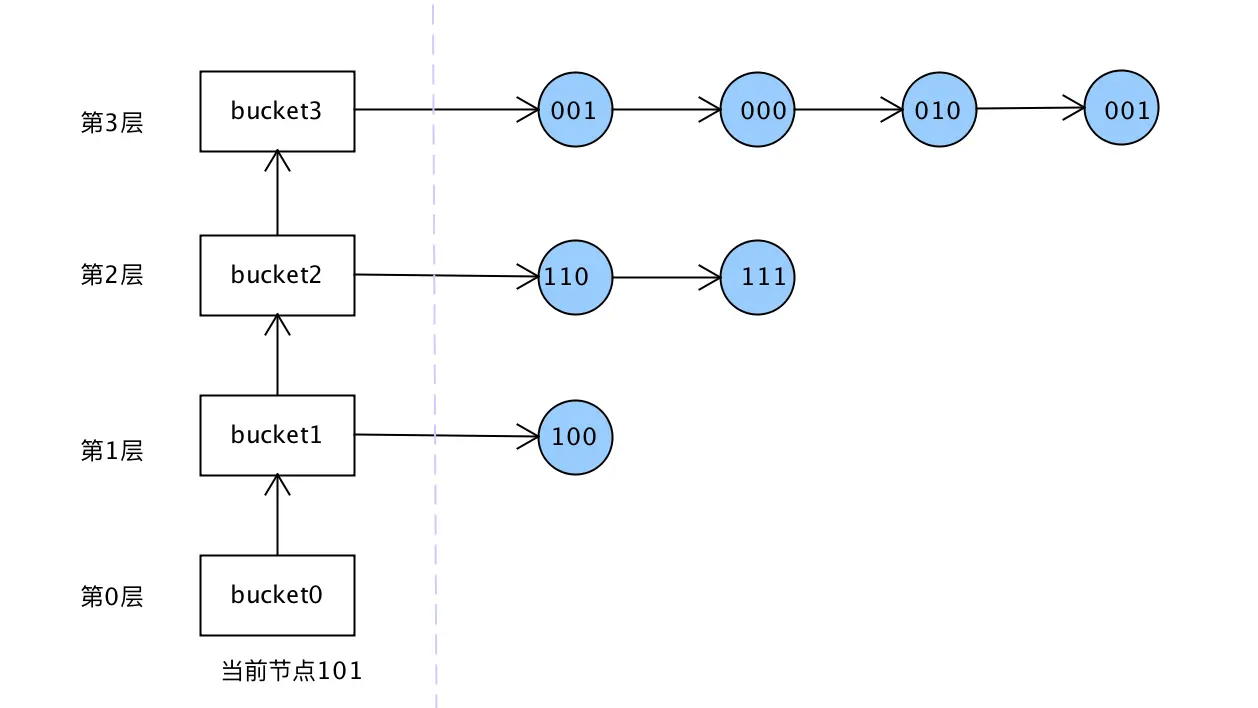
K桶覆盖距离的范围呈指数增长，离自己近的节点的信息多，离自己远的节点的信息少，从而保证了路由查询过程收敛。通过指数划分空间，因此N个节点的KAD网络最多只需要logN步查询就可以准确定位到目标节点。
KAD的UDP通信协议
Kad网络中节点通信基于UDP，有4个主要通信协议：
- Ping：探测节点是否在线
- Pong：响应Ping
- FindNode：向某个节点查询与目标节点异或距离接近的节点
- Neighbours：响应FindNode，会返回与目标节点ID距离接近的K桶中的节点
通过这4个命令可以实现新节点加入、K桶更新等机制。
K桶初始化流程
节点u加入KAD网络时，首先和一个已在网络中的公共节点w取得联系。
先将w加入K桶，再向w执行FindNode命令查询最接近自己的节点，将获取到的节点更新入K桶。（与此同时也是将自己的信息发布到其他节点的K桶）
最初u的路由表是单一的K桶，覆盖范围是整个ID空间，在学习到新的节点信息后根据其ID前缀插入/分裂对应K桶。具体规则：K桶没满就直接插入，如果满了且K桶覆盖范围包含了节点u的ID，则将K桶分裂成两个大小相同的新K桶，并对原K桶内的节点信息，按照新K桶的前缀值进行重新分配；如果K桶满了却没有覆盖u的ID，则直接丢弃新节点。
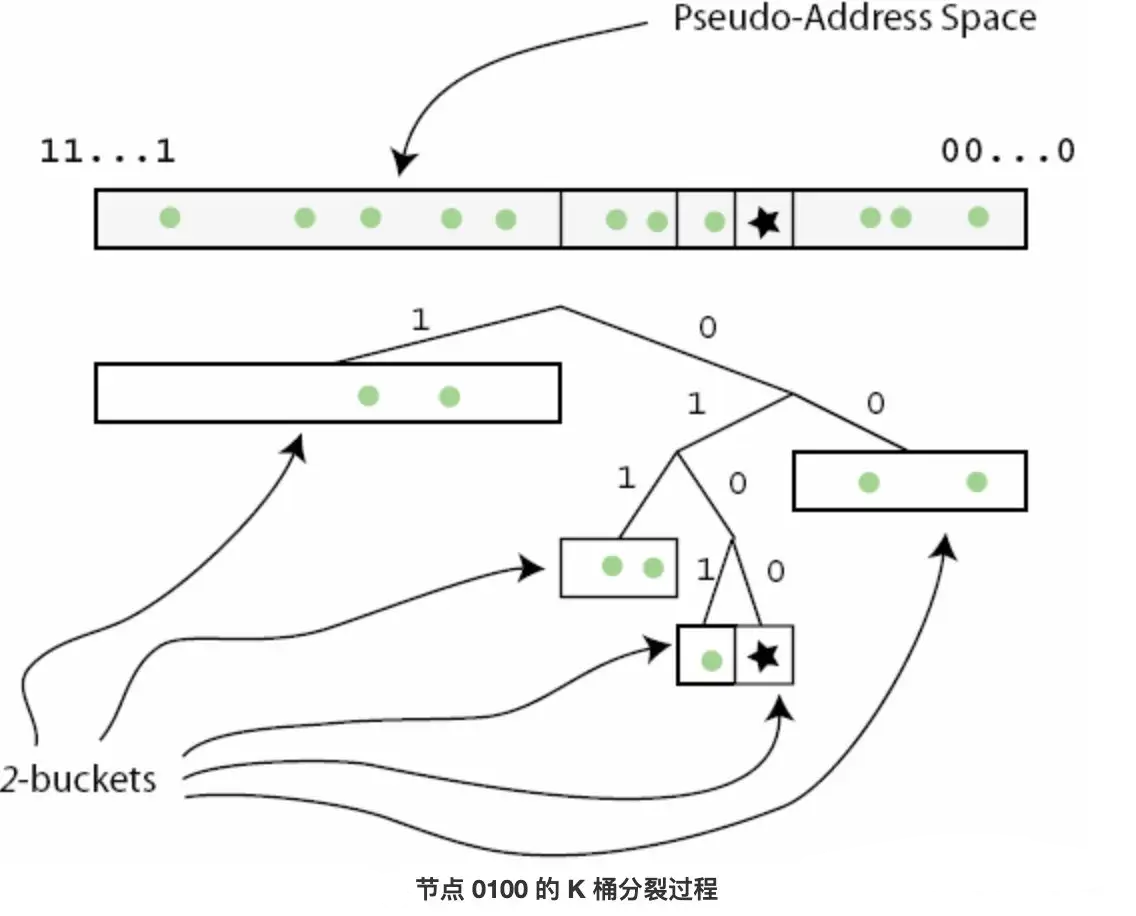
除此之外，初始化还会随机生成目标节点，通过找其临近节点去更新K桶
这一部分还是觉得存在逻辑问题，仅作参考
- 系统初次启动随机生成本地节点NodeID，记LocalId。
- 系统读取公共节点信息，PING-PONG握手后加入K桶。
- 系统每7200ms刷新一次K桶。（刷新是在获取网络中已知节点的IP、NodeId、端口号等信息）
刷新流程：
a. 随机生成目标节点ID，记TargetId，令发现深度为0，并开始记录发现用时。
b. 计算TargetId和LocalId的距离，记D_lt。
c. K桶中节点NodeId记KadId，计算KadId和TargetId的距离，记D_kt。
d. 从K桶中找出D_kt小于D_lt的节点，向这些节点发送FindNode命令，发现深度+1。
e. 节点收到FindNode命令后，从K桶中找出离目标节点更近的节点，使用Neighbours命令发回本地节点。
f. 本地节点收到Neighbours后，将收到的节点加入K桶。
g. 继续循环从c开始循环。若发现深度超过8，或刷新时间超过600ms，就不再循环。
节点离开网络不用发布任何信息，Kademlia协议的目标之一就是能够弹性工作在任意节点随时失效的情况下。为此，Kad要求每个节点必须周期性（一般是每1时）的发布全部自己存放的对数据，并把这些数据缓存在自己的k个最近邻居处，这样存放在失效节点的数据会很快被更新到其他新节点上。所以有节点离开了，那么就离开了，而且节点中的K桶刷新机制也能保证会把已经不在线的节点信息从自己本地K桶中移除。
K桶更新机制
节点收到PRC消息（Partial Route Calculation，网络路由变化时重新计算）时，发送消息的节点信息被用来更新对应K桶。（个人理解：这里的更新用于确定最可能在线的节点，两处排序不相关）
- 计算发送节点与当前节点距离。
- 根据距离确定位于K桶第几层。
- 如果已经存在于K桶中，将发送节点移到最前。
- 如果不在K桶中，且桶中数量小于K个，则添加节点信息到K桶末尾。
- 如果不在K桶中，且桶中的数量大于K个，先给桶中末尾节点发送PING消息：
如果收到回复，则忽略B节点。
如果未收到回复，则删除末尾节点，添加节点到最前。
K桶的更新机制依赖于一个理论：用户在线时间越长，它在下一时段继续在线的可能性就越高。通过将在线时间长的节点留在K桶中，提高了Kad网络的稳定性，以及减少了网络维护成本（无需频繁构建节点路由表）。这种机制的另一个好处是能在一定程度上防御DOS攻击，因为只有当老节点失效后，Kad才会更新K桶的信息，这就避免了新节点加入时泛洪路由信息。
为了防止K桶老化，所有在一定时间之内无更新操作的K桶，都会分别从自己的K桶中随机选择一些节点执行Ping操作。
上述这些K桶机制使Kad缓和了流量瓶颈（所有节点不会同时进行大量的更新操作），时也能对节点的失效进行迅速响应。
KAD的路由查询机制
假如节点A要查找ID为m的节点：
- 计算A的ID与m的距离。
- 确定距离所处K桶的层，从中取alpha个节点，若节点不够，从附近桶中获取。
- 同时向alpha个节点发送FindNode请求。（这里有点迷糊，A接收到的和发送的FindNode好像有所区别）
- 接收到FindNode的节点，如果ID是m则返回自身，否则从自己K桶中取距离最近的alpha个节点返回。
- A收到返回数据时，若其中有m则返回，否则向返回的alpha个节点发送FindNode请求，如此循环直至遍历所有节点。
BitTorrent和以太坊中alpha=3。
由于每次查询都能从更接近m的K桶中获取信息，这样的机制保证了每一次递归操作都能够至少获得距离减半（或距离减少 1 bit）的效果，从而保证整个查询过程的收敛速度为O(logN)，这里N为网络全部节点的数量。
如下为alpha=1的查找过程，演示了节点0011如何通过连续查询找到节点1110。连续查询中只有第一步的节点101是已知的，后面各步查询的节点都是上一步查询返回的更接近目标的节点，是一个递归过程。
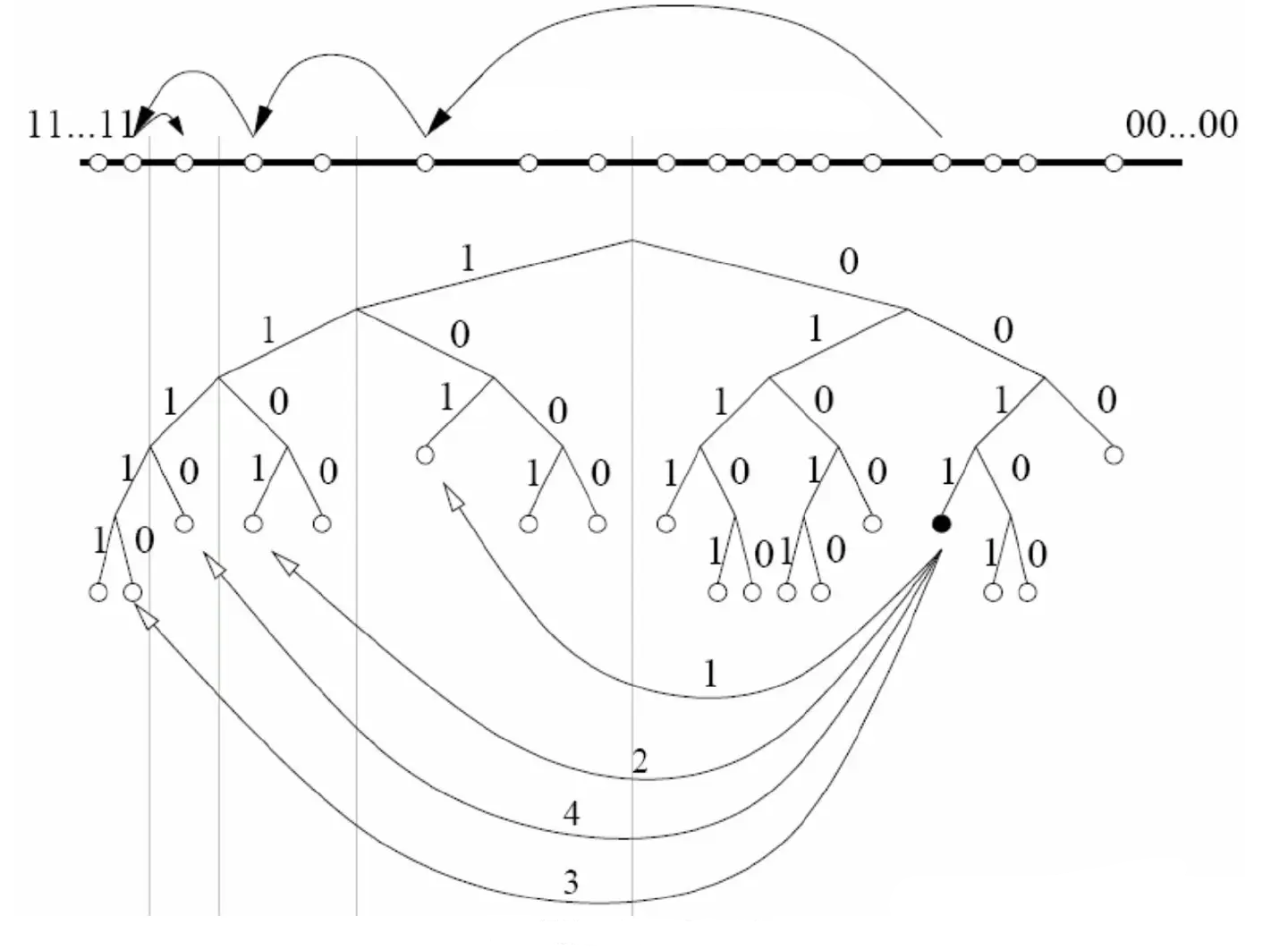
事实上，遍历完所有节点也不一定能找到m，因为ID为m的节点不一定存在网络中，不过最终倒可以得到许多接近m的节点。
基于这个思路，节点要查询数据<key, value>时，通过类似查询节点的操作，从K桶中选择k个最接近key的节点，发送FindValue命令（取存储的键值对数据）。接收命令的节点如果存有该数据就返回value，否则返回一个K桶中最接近key的一个节点信息。查询数据的节点如果收到的不是value，则对新返回的节点进行FindValue查询。
查询数据成功后，<key, value>会缓存到最接近key但没有key数据的节点上，下次相同查询就能够得到更快响应。在这种方式下，数据的缓存范围逐步扩大，使系统具有较佳的响应速度。数据在最近节点上的缓存时间为24h，但目标节点会向最近节点每1h发布数据，以更新数据超时时间。
数据存储
- 发起者首先定位k个ID最接近key的节点
- 向这k个节点发送STORE操作（存储数据）
- 执行STORE的k个节点每1h重发布自己所有的<key, value>数据
- 为限制失效信息，所有<key, value>在初始发布24h后过期
另外，为了保证数据发布、搜寻的一致性，规定在任何时候，当节点w发现新节点u比w上的某些 <key,value>对数据更接近，则w把这些<key,value>对数据复制到u上，但是并不会从w上删除。