区块链-密码学
区块链之加密原理总结(一)
密码学|数字签名方法:Schnorr签名
密码学|多重签名:基于Schnorr的MuSig方案
聚合签名、门限签名、Multisigs 和多签名
非对称加密基础
对称密钥线上分配秘钥时可能被拦截,而采用非对称秘钥,公钥公开,私钥自留,则降低秘钥泄露的风险。
各种加密传输的问题
发送节点A、接收节点B
1. 公钥加密
A使用B公钥对明文加密,传输,B使用B私钥解密得到明文。
问题:
- 消息源无法验证:B公钥是公开的,黑客可以假冒A
- 无法解决消息篡改
2. 私钥加密
A使用A私钥加密,传输,B使用A公钥解密。
问题:
- A公钥是公开的,密文被拦截后可以拿到明文,密文形同虚设
3. 双重加密 - 先公钥加密后私钥签名
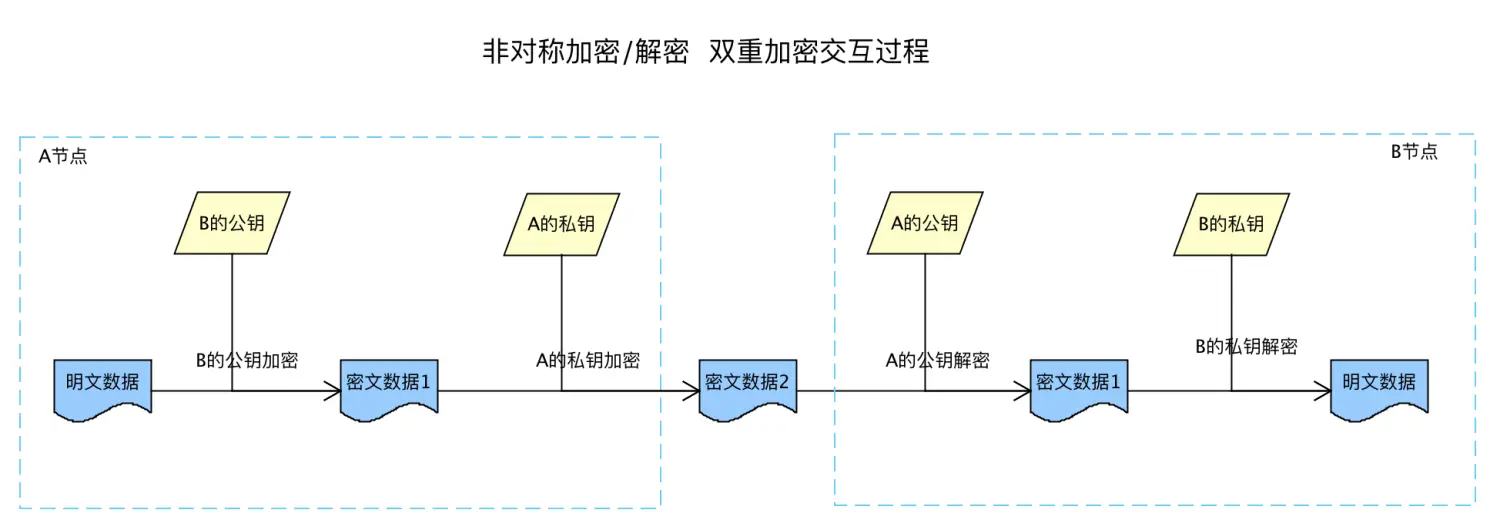
问题:
- A公钥公开的,虽说双重加密,其实外层加密无效
- 两次非对称加密,性能低
4. 双重加密 - 先私钥签名后公钥加密
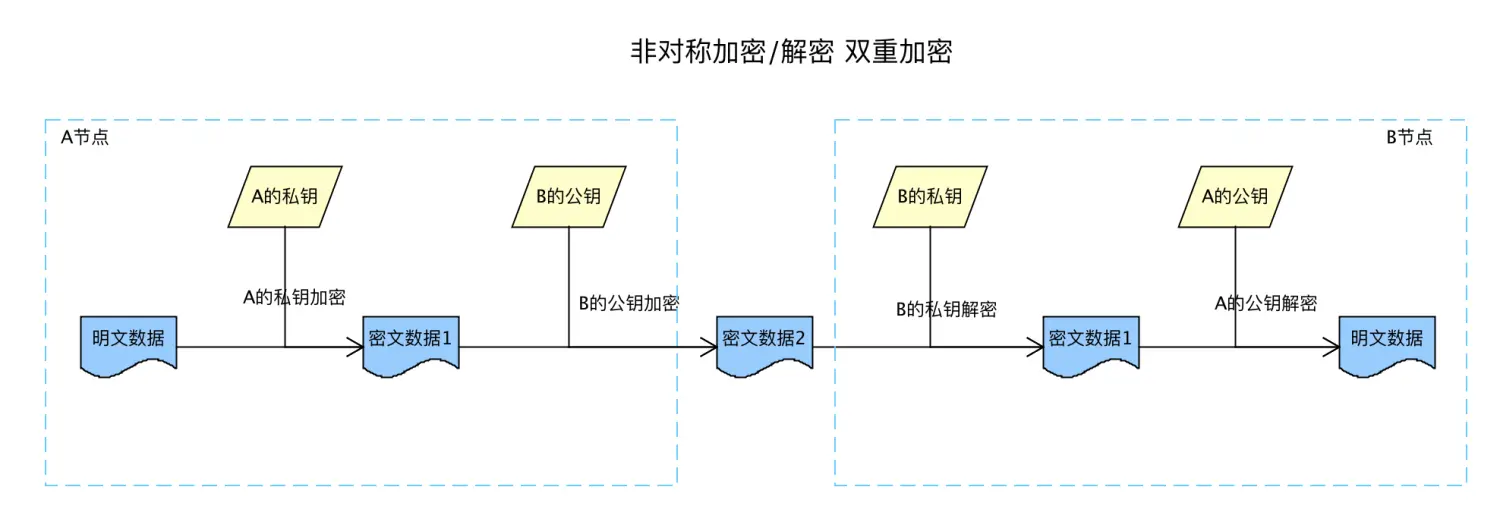
密文2只有用B的私钥才能解密,B在解密后能确定密文1来自A
问题:
- 两次非对称加密,性能低
消息认证
为防篡改,引入消息认证
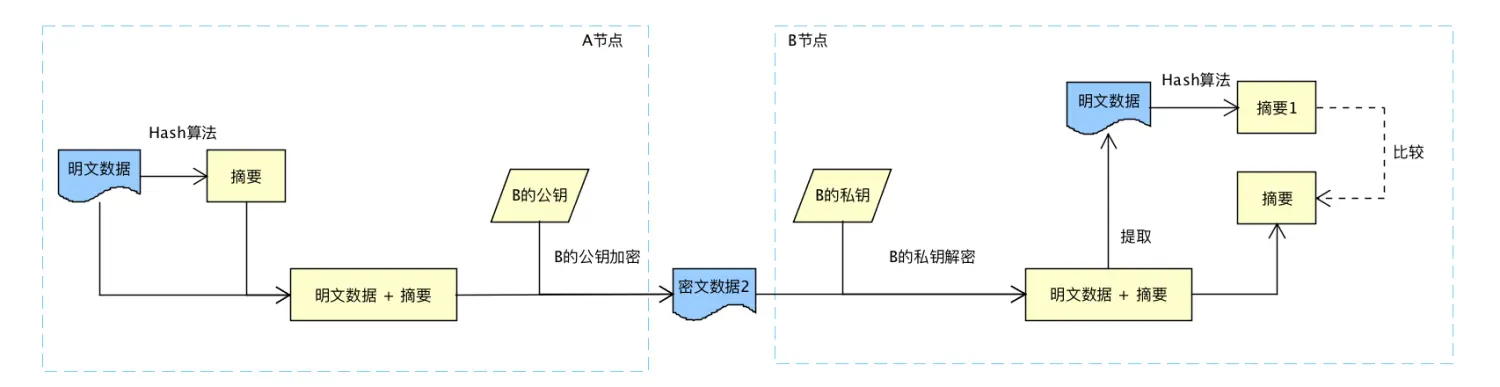
传输中如果密文2被篡改,摘要1和摘要对不上。
问题:
- 没有签名,A可能抵赖不是自己发的
消息签名
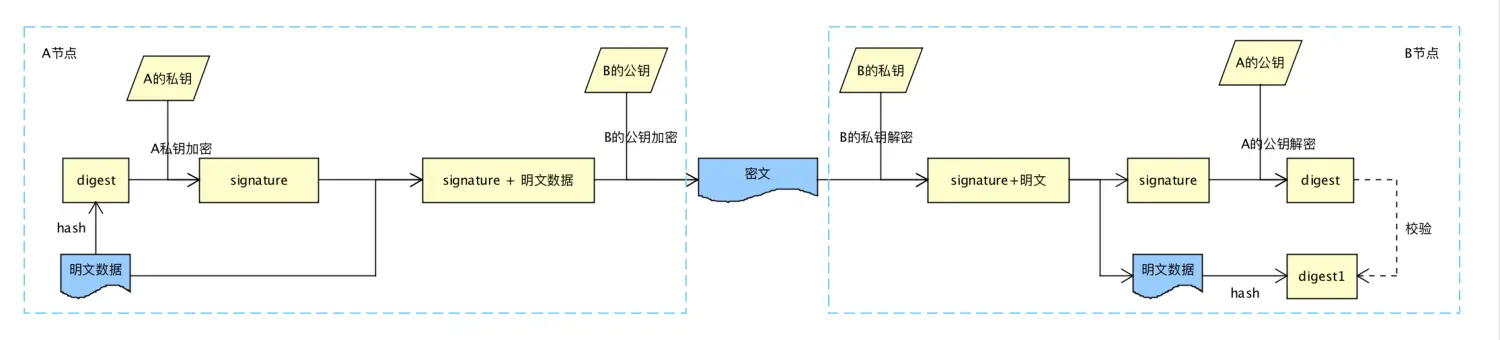
数字签名在区块链中的目标:
- 证明所有权,并为花费资金提供授权
- 证明不可否认性,授权的证据不可否认
- 证明签名的交易没被篡改,也无法被篡改
混合加密-不变的共享对称密钥
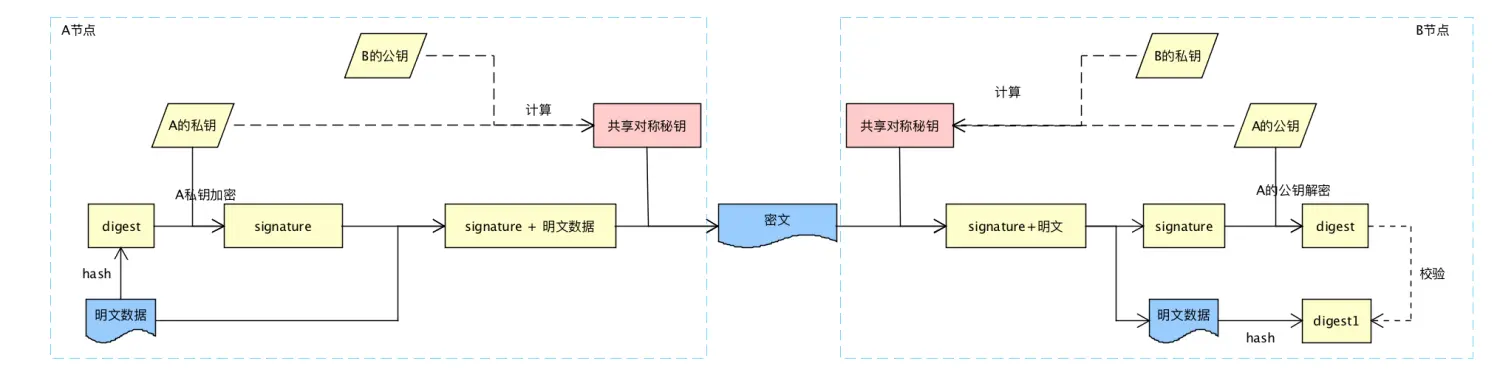
为解决非对称加密的性能问题,往往采用混合加密。
共享对称密钥的生成可以基于ECDH原理,发送方使用自己的私钥和对方公钥计算共享对称秘钥,加密数据传输后,接收方使用自己私钥和对方公钥计算共享对称秘钥解密。
问题:
- 秘钥固定不变,为增强安全性,最好每次交互都生成一个临时的共享对称密钥。
混合加密-随机的共享对称密钥
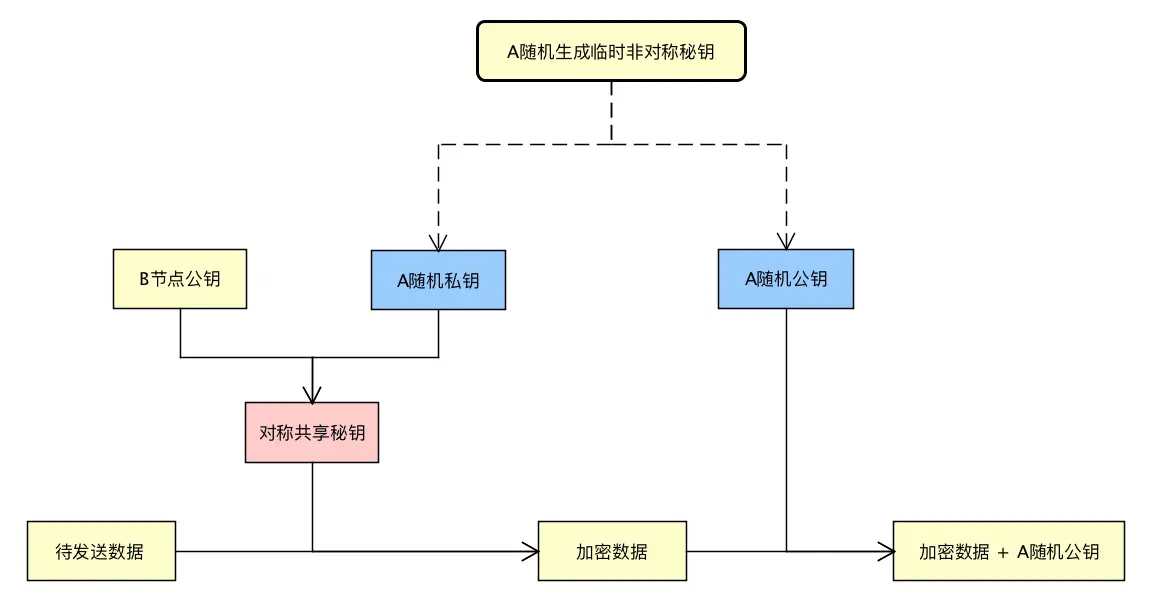
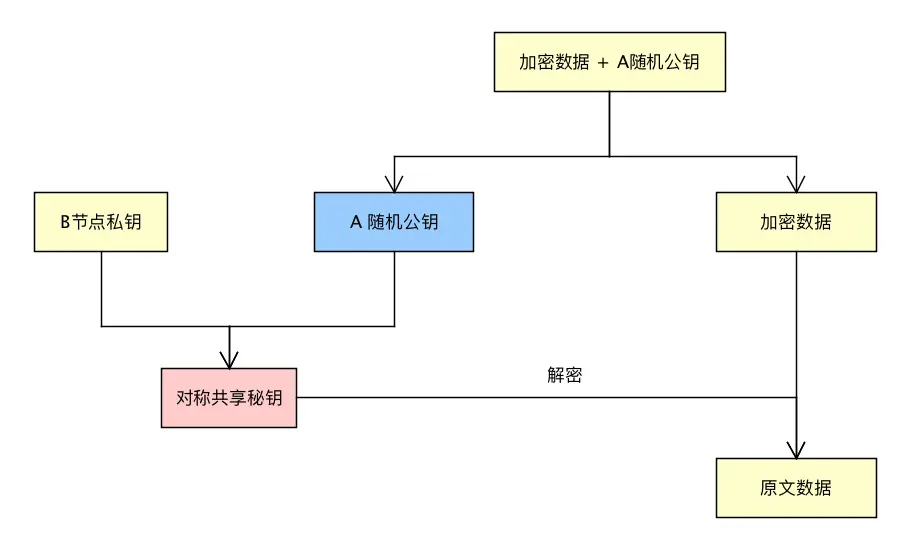
其他
事实上除了以上加密问题,还会存在如重放攻击(消息加Nonce)、彩虹表(KDF机制抵抗)的问题等。
根据传输数据的安全等级选不同安全程度的加密方案。
基于ECC的加密套件
密码套件概念
密码套件是网络协议的概念,主要包括身份认证、加密、消息认证、秘钥交换、伪随机数等算法组成。
- 秘钥交换算法:如ECDHE、RSA,主要用于客户端和服务端握手时如何进行身份验证
- 消息认证算法:如SHA1、SHA2、SHA3,主要用于消息摘要
- 批量加密算法:如AES,主要用于加密信息流
- 伪随机数算法:如TLS 1.2中的伪随机函数使用MAC算法的散列函数生成一个主密钥(连接双方共享的一个48字节的私钥),主密钥在创建会话密钥时作为一个熵来源。
网络涉及的加密
网络中一次消息的传输一般在4个阶段分别加密,保证消息安全、可靠传输
- 握手/网络协商阶段:如RSA、DH、ECDH
- 身份认证阶段:如RSA、DSA、ECDSA(ECC加密,DSA签名)
- 消息加密阶段:如DES、RC4、AES
- 消息认证阶段/防篡改阶段:如MD5、SHA1、SHA2、SHA3
ECC、ECDSA、ECDH、ECIES介绍
- ECC:Elliptic Curves Cryptography,椭圆曲线密码编码学。一种根据椭圆曲线上点倍积生成公钥、私钥的算法。用于生成公私钥
- ECDSA:一种数字签名算法,ECC和DSA的结合,签名过程和DSA类似,不过签名采用算法是ECC。有效的数字签名能够使接收者确认消息由发送者创建,发送者也不可否认。主要用于身份认证
- ECDH:基于ECC算法的霍夫曼树秘钥,通过ECDH,双方可以在不共享任何秘密的前提下协商出一个共享密钥(ECC算法生成对称秘钥),并且该秘钥是为当前通信暂时随机生成的,通信中断秘钥失效。主要用于握手
- ECIES:一种混合加密方案(混合对称加密、非对称加密、签名技术等一起使用),可以使用不同类型函数:秘钥协商函数(KA)、秘钥推导函数(KDF)、对称加密方案(ENC)、哈希函数(HASH)、H-MAC函数(MAC)
ECC算法
Wolfram MathWorld:一条椭圆曲线就是一组被 y^2 = x^3 + ax + b 定义的且满足 4a^3 + 27b^2 ≠ 0的点集。满足条件保证了曲线不包含奇点。
所有非对称加密的基本原理基于一个公式K=k*G(K公钥,k私钥,G代表选取的基点)。非对称加密算法要保证公式不可逆。
ECC核心思想,是在曲线上取一个基点G,之后在曲线上随机取一个点k(私钥),计算K(公钥,也在曲线上),并且保证不可逆(不可由K推出k)。
假如选一条曲线,a=-3,b=7,要如何计算K=k*G呢?
首先要理解椭圆曲线上加法和乘法的运算体系(比二元运算中的+和*要更抽象)。一条直线与椭圆曲线交于三个点P、Q、R,定义P+Q+R=0(0不是坐标轴上的0,而是ECC里定义的无穷远点),因此P+Q=-R,-R与R关于x轴对称。由此定义了ECC的加法。
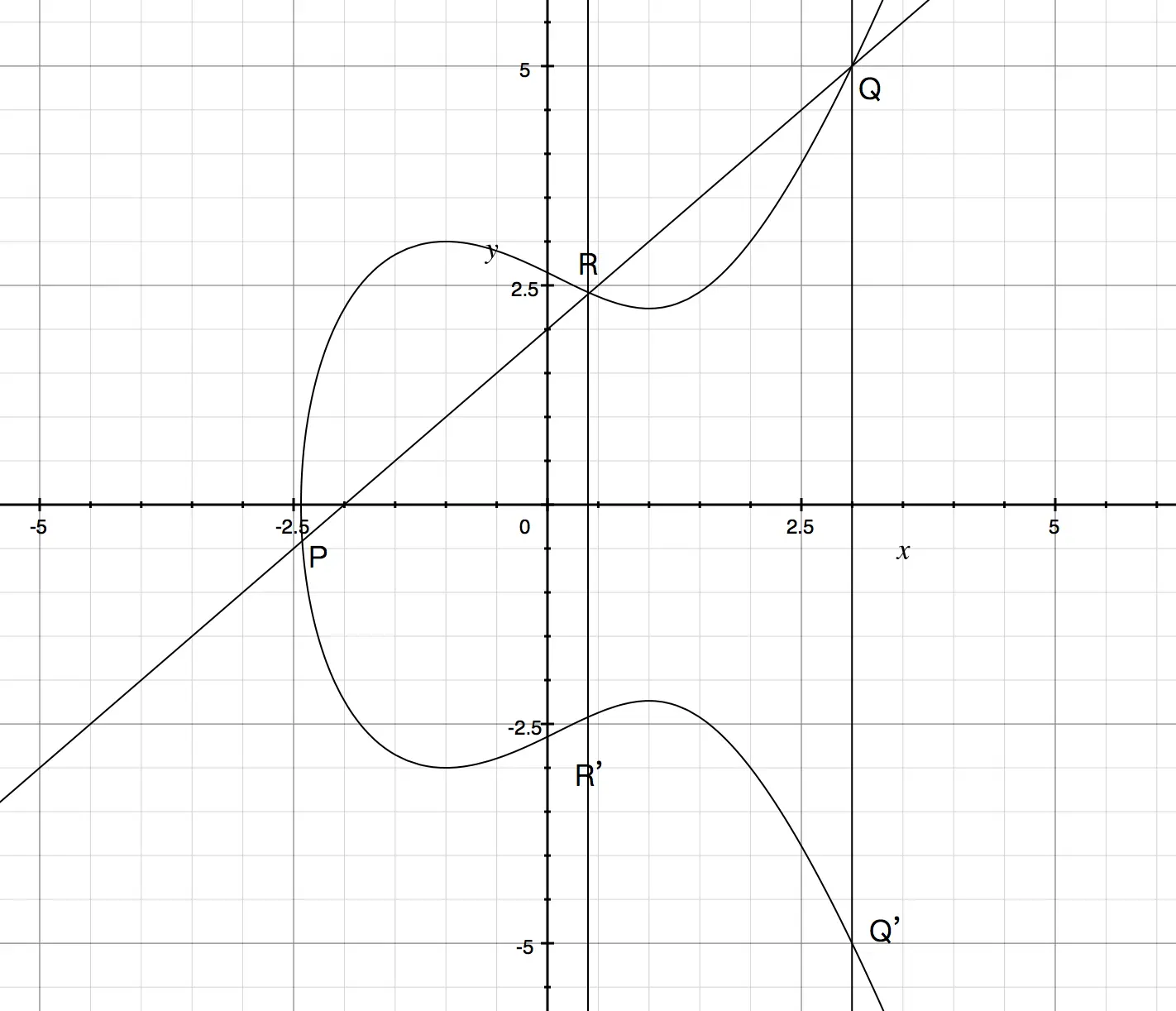
如果直线只与曲线有两个交点(可知直线是曲线的切线),即P和R重合了,P=R,那么P+R+Q=0变成2P+Q=0,即2*P=-Q。由此定义了ECC上一点与2的乘法。
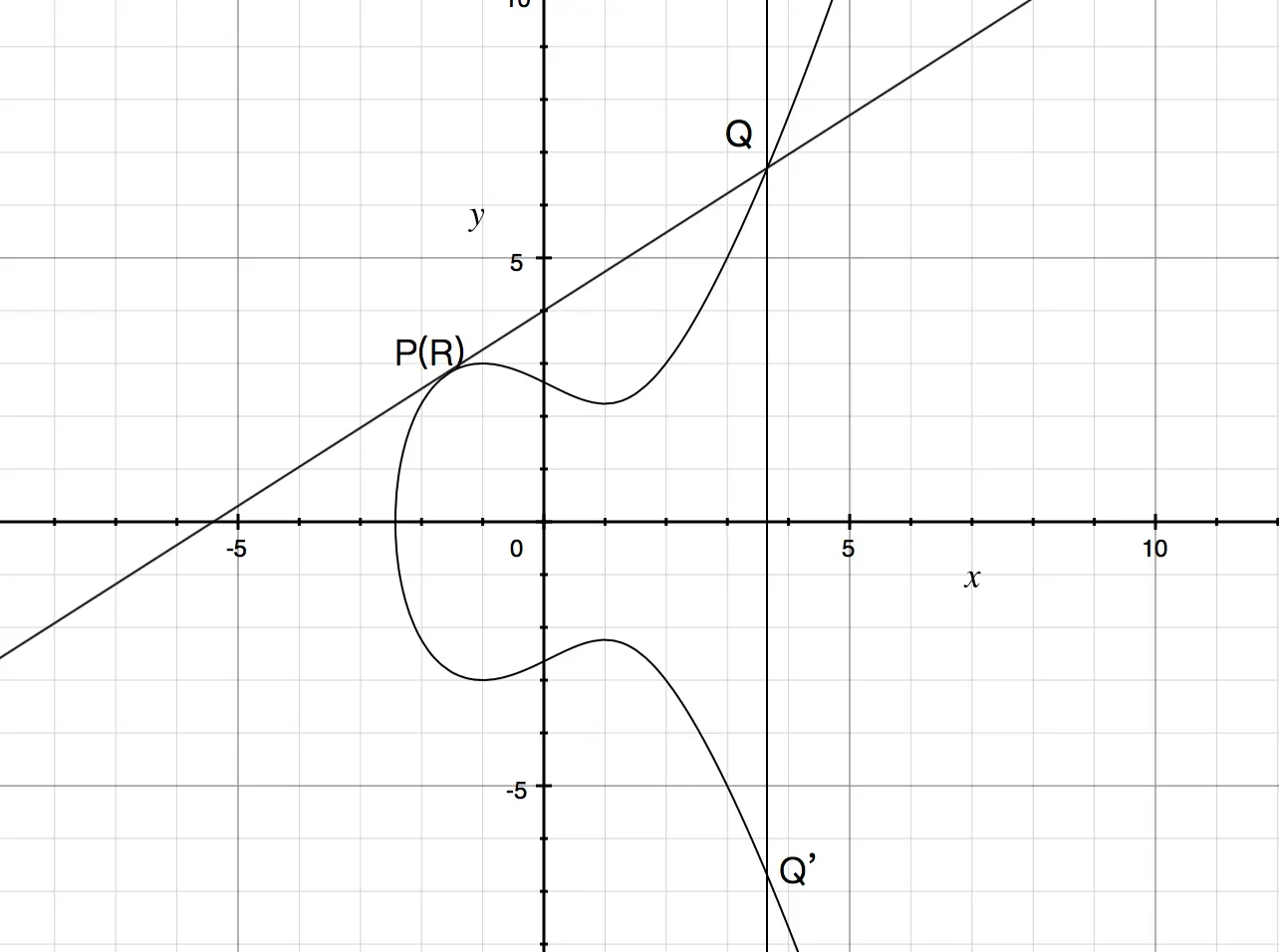
如果要ECC上一点要和任意整数相乘,也就是k*P,那么可以使用点倍积算法,将随机数k描述成二进制来计算。例如k=151,由于已知2*P的计算方法,自然可以解出2*2*...2*P,再根据ECC加法得到最终结果。
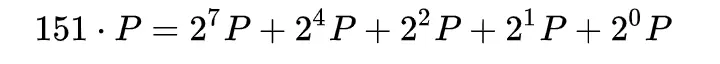
这个过程是不可逆的,知道k和P当然可以知道K,但是只知道P和K是难以知道中间经历了多少次k,因为k的取值范围太过庞大。理论上通过足够庞大的彩虹表应该是可能提前计算好k和K的对应关系的,但是有太多方法可以让k的范围变得更大,要准备好这张彩虹表几乎不可能。
ECDSA算法
ECDSA和DSA、RSA类似,都是私钥签名,公钥验证,不过采用了ECC算法。
根据ECC,基点G,私钥k,公钥K=k*G
签名过程:
- 生成随机数R,计算RG=(x,y)
- 根据R、消息M的哈希值H、私钥k,计算签名S=(H+kx)/R
- 将M、RG、S发给接收方
签名验证过程:
- 接收到M、RG、S
- 计算出M的哈希值H
- 根据发送方公钥K,计算RG'=(H+kx)G/S=HG/s+kGx/S=HG/S+Kx/S,对比验证是否RG和RG'相等
ECDH算法
非对称加密中的“椭圆曲线迪菲-赫尔曼密钥交换”(Elliptic Curve Diffie-Hellman, ECDH) 常用于生成共享密钥,用于后续对称加密通信。
以Alice和Bob通信为例,双方基于同一套ECC生成的公钥K和私钥k,且共同的基点G=(x,y)
生成秘钥阶段:
- Alice使用公钥算法KA=ka*G,生成了公钥KA和私钥ka,并公开公钥KA
- Bob使用公钥算法KB=kb*G,生成了公钥KB和私钥kb,并公开公钥KB
计算ECDH阶段:
- Alice利用公式Q=ka*KB计算出秘钥Q
- Bob利用公式Q'=kb*KA计算出秘钥Q'
事实上Q=ka*KB=ka*kb*G=kb*KA=Q'
完整流程:
- 双方各自生成密钥对:每方都有自己的私钥和对应的公钥。
- 生成共享密钥:
- 发送方使用自己的私钥和接收方的公钥,通过ECDH算法生成共享密钥,用于加密数据。
- 接收方使用自己的私钥和发送方的公钥,通过相同的ECDH算法生成相同的共享密钥,用于解密数据
- 加密通信:共享密钥用于对称加密和解密消息,因为对称加密的计算速度比非对称加密更快。
这种机制的安全性基于椭圆曲线离散对数问题,计算共享密钥过程中,私钥从未暴露,因此即使攻击者截获了双方的公钥,也无法计算出共享密钥。
核心特点:
- 密钥协商:双方独立生成相同的共享密钥,而无需直接交换密钥。
- 安全性:即使公钥暴露,私钥的安全性确保共享密钥的安全。
- 效率:生成的共享密钥可用于快速对称加密。
这种方式广泛应用于安全通信协议中,如TLS/SSL,用于安全的密钥协商和数据传输。
Schnorr签名算法
ECDSA签名的验签环节包括反转(1/s)和两点乘法的运算,计算量大,可以优化。另外ECDSA简单多签名情况下,需要对包含的多个签名都进行验证。
1. 签名
假设密钥对(x,X=x*G),则消息m的Schnorr签名为**(R,s)**
R=k*G
s=k+H(R,m)*x
k为随机生成的私钥,签名(R,s)中s本质上是“私钥x的所有者已签署消息m”的证明,而R作为一次性公钥用于和普通公钥X一起验证签名。
2. 验签
验签者已知m、X、(R,s)
要检查:s*G ?= R+H(R,m)*X
3. 一次性随机数k的重要性
如果使用相同密钥签署两条不同消息(两次的随机数k一样),会泄露整个私钥!
假如攻击者已知
- 公钥X
- 重用随机数k所生成的R
- 签署的第一条消息m1、签名s1
- 签署的第二条消息m2、签名s2
s1-s2 = (k+H(R,m1)*x) - (k+H(R,m2)*x) = H(R,m1)*x - H(R,m2)*x = (H(R,m1)-H(R,m2))*x
x = (s1-s2)/(H(R,m1)-H(R,m2))
s1、s2、R、m1、m2都已知,显然x会泄露
4. 与ECDSA比较
- Schnorr签名比ECDSA更小、更块
- Schnorr签名是线性的,两个实体签署同一消息后签名可以聚合并验证。这是Schnorr与其他签名方案的关键区别
因为线性,若令聚合随机值R=R1+R2,则可实现基于Schnorr的多签名方案
Sign(x1, k1, m)+Sign(x2, k2, m)
=(k1+H(R, m)*x1)+(k2+H(R, m)*x2)
=(k1+k2)+H(R,m)*(x1+x2)
=Sign(x1+x2, k1+k2, m)
原理类似如此,不过还需解决恶意密钥攻击的问题,具体参考下文的**《基于Schnorr的MuSig方案》**
为了实现聚合签名,则将所有签名相加,验证者不用针对各个交易签名进行验证,只需验证总签名:
(s1+...+s1000)*G=(R1+...+R1000)+(H(R1,m1)*X1+...+H(R1000,m1000)*X1000)
BIP 340 :“尽管有这些优势,几乎没有缺点。”
Schnorr 是基于椭圆曲线的最简单的签名方案,比特币将只会从它中受益。
多重签名技术
简介
多重签名要求多个不同私钥来授权一笔交易,增加了交易安全性。
要素:
- 多个私钥
- 签名阈值:需要达到多少个授权者的签名,如2-of-3多签钱包要求至少两个签名
- 多签交易:交易的签名数量达到签名阈值
应用:
- 保护个人钱包安全
- 用户DAO,集体决策
- 商业应用程序,多重签名确保公司资金安全(如公司董事会共同控制公司资金)
Gnosis Safe是一个运行在以太坊上的智能合约钱包,具有多重签名功能,允许用户定义所有者/签名者账户列表以及确认交易所需的签名者阈值数量。
多签名、聚合签名、门限签名的区别
1. 简单的多签名
n个用户各有一对独立的公私钥,对同一个消息分别进行签名,这个消息的有效签名是n个用户签名的集合,最终验证消息时需要用到每一个签名者的公钥。
消息的签名证据中包含了n个签名和n个相应的公钥,交易的体积和处理成本随n增大而线性上升,交易费用昂贵。
如比特币中OP_CHECKMULTISIG(OP_CMS)操作。实际上OP_CMS还支持如m-of-n等更多操作,不过仍存在交易体积和费用问题,另外没有隐私,所有参与者都是公开的。
2. 多签名(multi-signature)
在简单的多签名基础上,将n个用户签名聚合成一个公开的签名,对外也只公开一个公钥。
和聚合签名类似,不过只能对同一个消息进行多签。
3. 聚合签名(aggregate signature)
n个不同签名者分别对n条不同消息签名,得到n个签名,再聚合成一个签名。提供更快的验证速度,节省空间和带宽。
签名聚合机制主要分两种:
- 一般化聚合:每个用户i对自己的消息Mi创建签名Si。任何人都可以使用公共的聚合算法,将N个签名压缩成一个聚合的签名。(如矿工将区块内每笔交易的签名去聚合成一个签名)
- 序列化聚合:用户1签名M1得到S1,用户2再用S1和M2得到S2,以此类推,直到用户n用S(n-1)和Mn生成最终签名。序列化签名聚合只能在签名流程中完成。
有许多被称为聚合签名的签名方案,如Schnorr签名、基于格的签名、基于配对的签名(比如BLS方案,已在Difinity和Algorand等区块链应用),不过多数情况下它们都被用于对同一条消息进行(用作多签名的案例更合适)。
4. 门限签名(threshold signature)
m-of-n门限签名,n个签名者中的任意m个即可代表全体。签名用一个由参与者公钥组合成的群体公钥来验证。
门限签名不会暴露参与生成签名的成员。
目标是控制签名能力(m>1),和消除单点故障(n>1)。
基于Schnorr的MuSig方案
MuSig是一个Schnorr多签名方案,由Blockstream提出,无论签名者数量多少,通过密钥聚合产生一个和普通Schnorr签名无法区分的签名(签名者保密,无法辨别具体由谁签名),且验证与普通Schnorr签名完全相同。
假设n个签名者X1、X2、……、Xn对一条消息m共同签署,通过MuSig生成一个单一Schnorr签名(R,s)
1. 朴素Schnorr多签名
针对签名者i
- 私钥xi
- 公钥Xi=xi*G
- 一次性私钥ki
- 部分签名Ri=ki*G
- 部分签名si=ki+H(X,R,m)*xi
- 朴素Schnorr多签名中每个签名者需公布自己的公钥Xi,从而得到聚合密钥X=X1+X2+...+Xn
- 签名者还要生成和分享自己的部分签名Ri,得到部分聚合签名R=R1+R2+...+Rn
- 每个签名者计算部分签名si=ki+H(X,R,m)*xi,公布si并计算部分聚合签名s=s1+s2+...+sn
=(k1+...+kn) + H(X,R,m)*(x1+...+xn)
=k+H(X,R,m)*x
朴素Schnorr多签名(R,s),涉及变量
- 聚合私钥x
- 聚合公钥X
- 聚合一次性私钥k
- 聚合部分签名R
- 聚合部分签名s
验证者验签:s*G ?= R+H(X,R,m)*X
朴素Schnorr多签名方案能够聚合多个签名,但很遗憾,会受到恶意密钥攻击(流氓密钥攻击)
2. 恶意密钥攻击
如果我的公钥是X1,但我撒谎将X1'=X1-X2-...-Xn公布给其他签名者,聚合公钥X=X1'+X2+...+Xn=X1,我便可为所欲为。
如果大家要求我证明我对“我所声明的公钥X1'”拥有私钥,将能阻止我的恶意密钥攻击,但是我还可以对Ri发起同样的攻击来控制聚合一次性私钥k,在收集完其他签名者的部分签名si后,可以计算出聚合签名s=k+H(X,R,m)*x,同样可以算出x。
3. 改进方案
为抵御对聚合随机数R发起的恶意密钥攻击,要求先广播随机数Ri的哈希值ti=H(Ri),在看到所有签名者的ti后再揭示Ri,即哈希承诺。
对聚合签名公钥X做同样方案是不切实际的,因为公钥是公开的且重复使用的。
为抵御对聚合公钥X发起的恶意密钥攻击,令X=a1*X1+a2*X2+...+an*Xn,ai=H(L||Xi),L为所有公钥集合的某种编码。由此就很难通过其他签名者的公钥计算出一个X1',使得X=X1'。
经过这种改动后,需要调整公式si=ki+H(X,R,m)*ai*xi
s=s1+s2+...+sn
=(k1+...+kn)+H(X,R,m)*(a1*x1+...+an*xn)
=k+H(X,R,m)*x
MuSig签名包括三个阶段:
- 所有签名者发送承诺ti
- 所有签名者揭示Ri,并验证ti=H(Ri)
- 所有签名者计算并发送部分签名si
最终可以计算出Schnorr签名(R,s)
改进的MuSig2方案
每个参与者有一对公私钥,由随机数x∈Z(私钥)计算X=g^x(公钥)来生成(g为一个循环G上的生成点)
通过两轮通信让m个用户生成m个中间签名,结合生成一个最终签名,然后用所有用户聚合的公钥来验证。
亮点:
- 可安全地并行签名
- 可聚合密钥
- 生成的最终签名为常规的Schnorr签名
- 从MuSig三轮通信变为两轮
- 验签时的复杂性和普通Schnorr签名相似
缺:
- 无法像门限签名可指定签名阈值
默克尔多重签名(Merkle Multisig)
要使多签名方案更灵活,可以修改算法使之转为一种门限签名方案。
使用一种默克尔树来包含所有可能的签名者组合的密钥,通过遍历来检查一组签名是否为有效的签名群组。
n为参与者数量,m为阈值,默克尔树包含元素数量为C(n,m)。
使用默克尔树的方法可以和MuSig2、BLS等任意多签名方案结合。在比特币的Taproot升级中以MAST(merkelized abstract syntax trees)为名,使用默克尔树来存储多个用户指定的、为花费该笔比特币需要满足的充分条件。所有可能组合的聚合公钥放在默克尔树的叶子节点,并将根放到锁定脚本中,使用比特币时提供一个签名和证明我们的公钥在默克尔树上的证据。
FROST门限签名
FROST使用一种准受信任的签名聚合者(SA)设置,设置的存在减少了带宽开销。聚合者为协助而设置,没有信息上的权限。SA要负责识别行为不轨的参与者,并在协议完成时发布群体签名。即使SA自身行为不轨,协议也可对抗适应型选择性明文攻击。恶意SA可以发起分布式拒绝服务攻击,也可以恶人先告状,但无法获得参与者的私钥,也无法使不合适的信息得到签署。
BLS门限签名
BLS签名过程不需要随机数,所有签名可以组合成单个签名,m-of-n的多重签名很简单实现,签名者间不需要多轮通信,签名比Schnorr签名或ECDSA签名小2倍,不是一对而是单曲线点。
1. 曲线哈希(哈希映射到曲线上的点)
ECDSA和Schnorr签名算法中对消息进行哈希后的结果是数字,而BLS签名算法则要将结果映射到椭圆曲线上的点。最简单的修改:哈希函数不变,将哈希值作为x在椭圆曲线上找点。由于通常椭圆曲线有2^256个点,而一个有效的x会对应两个一正一负的y坐标,因此在使用SHA-256算法下,有50%概率找不到对应点。
为确保能够在曲线上找到对应点,如果消息的哈希值在曲线上找不到对应点时,附加在消息体后的数值累加并重新计算。
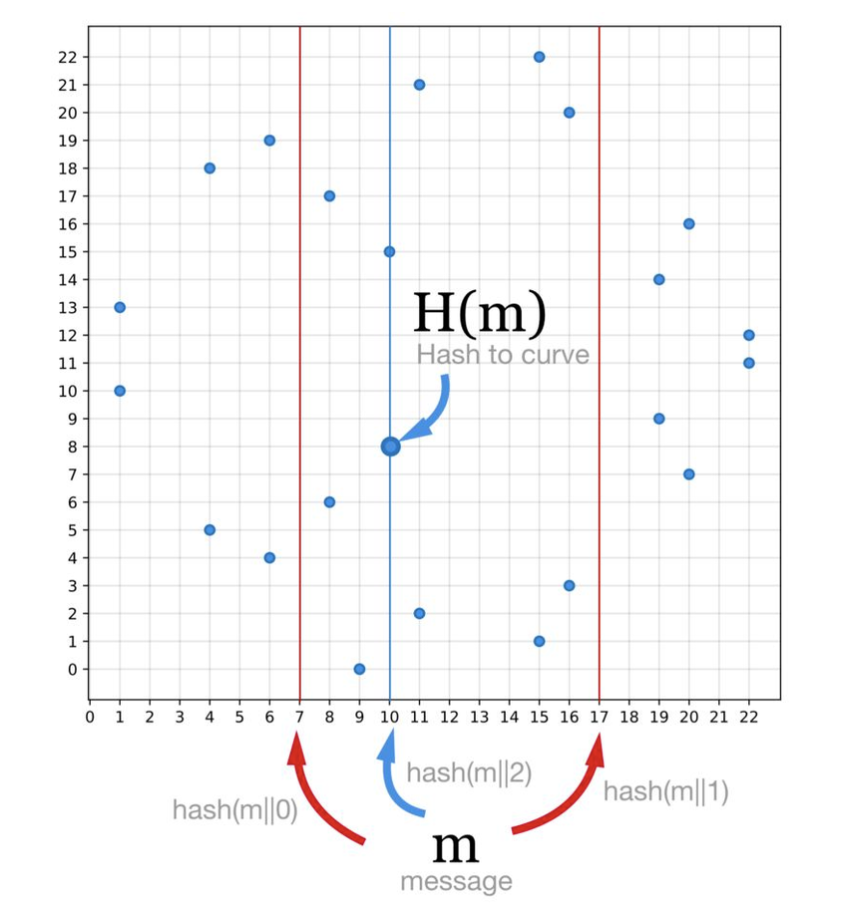
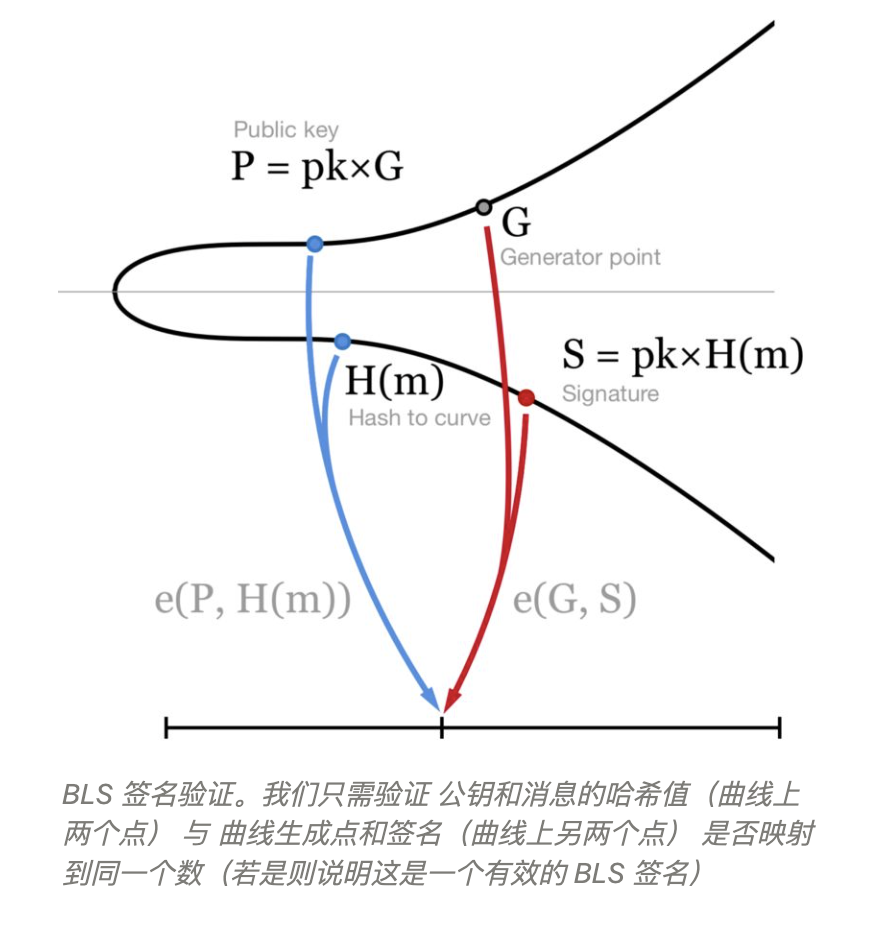
2. 曲线配对(曲线上两个点映射为一个数)
曲线配对函数:一种特殊函数e(P,Q)->n,将一条或两条不同的曲线上的两个点P和Q映射为一个数n。
函数具有特性e(x*P, Q) = e(P, x*Q)
由此e(a*P, b*Q) = e(P, ab*Q) = e(ab*P, Q) = e(P, Q)^(ab)
3. 签名应用
私钥pk、公钥P=pk*G、签名消息m
签名S=pk*H(m),H(m)为曲线哈希,将m映射到曲线上一点
BLS不需要随机数,不需要额外通信,仅仅是哈希结果乘以公钥,结果是曲线上的点,用压缩的序列化格式保存只占33字节。
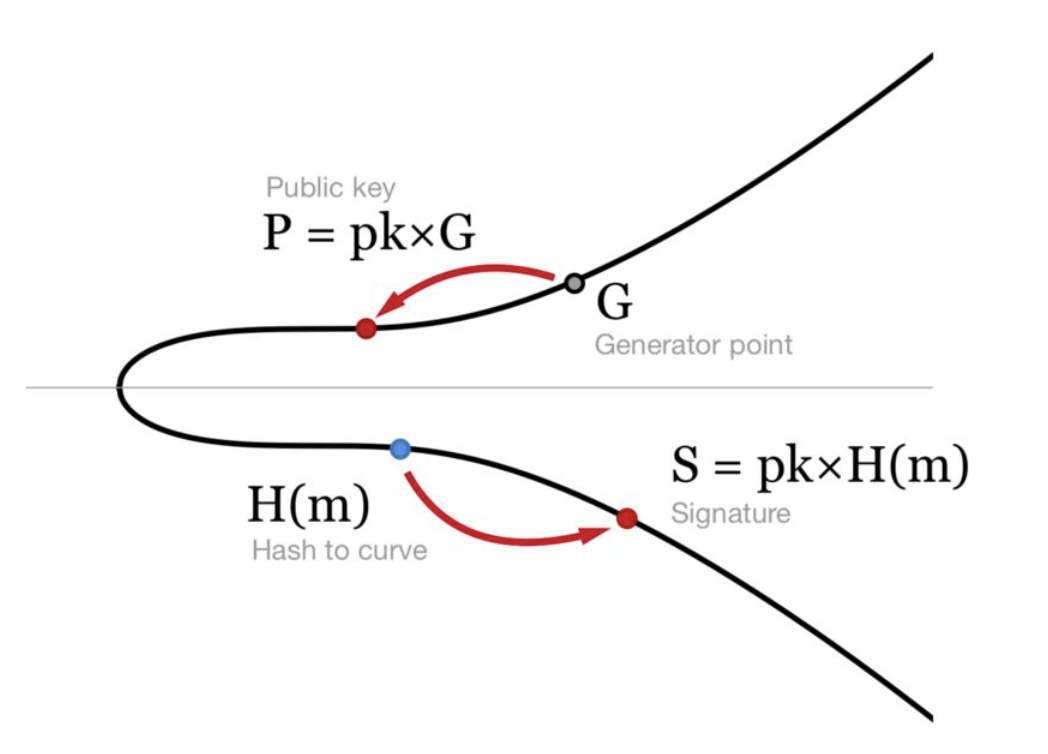
使用P验签,e(P, H(m)) = e(G, S)
4. 多签名
针对同一消息,所有签名者生成的签名聚合
令公钥的聚合P=P1+...+Pn
令签名的聚合S=S1+...+Sn
验签:
e(G, S) = e(G, S1+...+Sn)
= e(G, S1) * ... * e(G, Sn)
= e(G, pk1 \ * H(m)) * ... * e(G, pkn * H(m))
= e((pk1+...+pkn) * G, H(m))
= e(P, H(m))
和Schnorr多签名一样,需要防御恶意密钥攻击。一种方法是要求签名者用私钥签名公钥以证明拥有对应公钥,一种是加入非线性系数使攻击难以发起。
P=a1*P1+...+an*Pn
S=a1*S1+...+an*Sn
ai=H(Pi, {P1,...,Pn})
无需多轮通信,不依赖随机性。
5. 聚合签名
用在区块内每笔交易的签名聚合成一个签名
聚合签名S=S1+...+Sn
验签:
e(G, S) = e(G, S1+...+Sn)
= e(G, S1) * ... * e(G, Sn)
= e(G, pk1 \ * H(m1)) * ... * e(G, pkn * H(mn))
= e(P1, H(m1)) * ... * e(Pn, H(mn))
验签需要计算n次配对函数,但是区块签名大大减小。
6. 门限签名
已知
P=a1*P1+...+an*Pn
S=a1*S1+...+an*Sn
ai=H(Pi, {P1,...,Pn})
再公开地计算成员密钥MKi,每个MKi都是消息H(P,i)的有效n-of-n签名
假设共3个成员
MKi = (a1*pk1)*H(P, i)+(a2*pk2)*H(P, i)+(a3*pk3)*H(P, i)
e(G, MKi) = e(P, H(P, i))
假设现在pk1和pk3对一笔交易签名
S1=pk1*H(P,m)+MK1
S3=pk3*H(P,m)+MK3
MK1和MK3是彼此知道的,但是私钥pk只有自己知道
门限签名S'=S1+S3,子集聚合公钥P'=P1+P3
验签e(G, S')=e(P', H(P, m))*e(P, H(P, 1)+H(P, 3))
e(G, S')=e(G, S1+S3)=e(G, pk1*H(P, m)+pk3*H(P, m)+MK1+MK3) =e(G, pk1*H(P, m)+pk3*H(P, m))⋅e(G, MK1+MK3)=e(pk1*G+pk3*G, H(P, m))⋅e(P, H(P, 1)+H(P, 3))=e(P', H(P, m))⋅e(P, H(P, 1)+H(P, 3))
7. BLS签名应用场景
若要实现上述多重签名方案,需要先将资金发送到聚合公钥P对应的地址,并表示我们至少需要两个签名。
比特币中锁定脚本可能如:OP_2, OP_CHECK_BLS_MULTISIG,OP_2说明需要两个密钥签署。为了使用这个输出,需要提供解锁脚本:OP_1, OP_3, <P'>, <S'>,根据索引OP_1和OP_3可计算哈希H(P, 1)和H(P, 3)。
因此,对于任意m和n,需要:
- 锁定脚本中的一个聚合公钥P
- 参与签名者的一个聚合公钥P'
- 一个聚合签名
- 带签名者索引的m数字
通常地址只使用一次,每次都要运行设置阶段来为每组私钥生成一组新的成员密钥。更好的方法是一次就生成比如1000组成员密钥,这1000组用完再运行设置阶段重新生成。
8. 优缺
优点:
- 聚合公钥和签名的运算比验证便宜多,带来速度优势。
- 空间优势
缺点:
- 配对函数不高效,验签的复杂度高ECDSA一个数量级,验签1000笔交易的聚合签名需要进行1000次配对计算,可能比ECDSA对1000个单独签名验证还要慢,不过好处在于聚合签名空间占用很小
- 配对函数十分复杂,使用不当反受其累。一方面希望使用更高效的配对函数,又希望密钥信息暴露更少,二者矛盾。有一种针对椭圆曲线加密系统的攻击方法称为MOV攻击(以Menezes, Okamoto和Vanstone命名),它允许使用我们的魔法配对函数来降低系统的安全性。所以我们真的需要小心。
PBKDF2
基于密码的关键推导函数
盲签名
盲签名由大卫·乔姆提出,消息原内容对于签名者不可见,有效保护隐私。得到的盲签名可以对消息原内容以常规数字签名方式公开验证。
类比:将文件放入一封带有复写纸的信封内,密封,签名者在信封上签名,签名透过复写纸签到文件上。
其他
彩虹表:彩虹表是一种高效密码破解技术,主要用于逆向查找哈希值对应的原始密码。它通过预先计算大量哈希值与原始密码的对应关系,并存储在一个巨大的表中,从而在破解时避免了重新计算哈希值的过程,显著提高了破解速度。这种表可以破解包括MD5、NTLM在内的多种加密算法。尽管彩虹表非常强大,能快速破解密码,但它需要大量的存储空间。例如,Ophcrack是一个著名的彩虹表密码破解工具,支持多种哈希类型,且有免费和付费的彩虹表可供选择,适用于不同需求的密码破解场景。对于特别复杂的密码或未被预计算的哈希类型,彩虹表则无能为力。
BTC的椭圆曲线
在比特币中,椭圆曲线被用于生成公私钥对,其使用的椭圆曲线是 secp256k1。这个曲线的基点(也称为生成点,通常记为 G )是协议中固定的参数,用于计算公钥。
secp256k1 的基点 G 的坐标是一个椭圆曲线上的点,定义为:G = (x, y)
- x坐标:x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798) - y坐标:y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
(0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8)
secp256k1 的基本参数
- 曲线方程: y^2 = x^3 + 7
这表明 secp256k1 是一个简单的 Weierstrass 曲线,没有复杂的参数项。 - 有限域: p = 2^{256} - 2^{32} - 977
这是一个大素数,定义了椭圆曲线上的点计算是在这个域内进行的。 - 基点的阶数 n:n = 115792089237316195423570985008687907852837564279074904382605163141518161494337
这个值决定了标量乘法的循环周期,即私钥的选择范围。
基点 G 的作用
- 生成公钥:
私钥是一个随机选取的数 d ,公钥 P 是基点 G 通过标量乘法 d · G 计算得到的点。这使得私钥和公钥之间有明确的数学关系,但公钥推导私钥几乎不可能完成,保证了安全性。 - 加密和签名:
基点 G 是所有计算的起点,是整个比特币网络中生成密钥对和签名验证的重要基础。
比特币的椭圆曲线 secp256k1 的基点是一个固定且公开的点,用于确保密码学操作的标准化和安全性。它的选取保证了椭圆曲线运算的高效性和安全性,是比特币及其他加密货币体系的核心密码学元素。
以太坊中UDP通信的加密方案
H-MAC基本模型
H-MAC,Hash-based Message Authentication Code
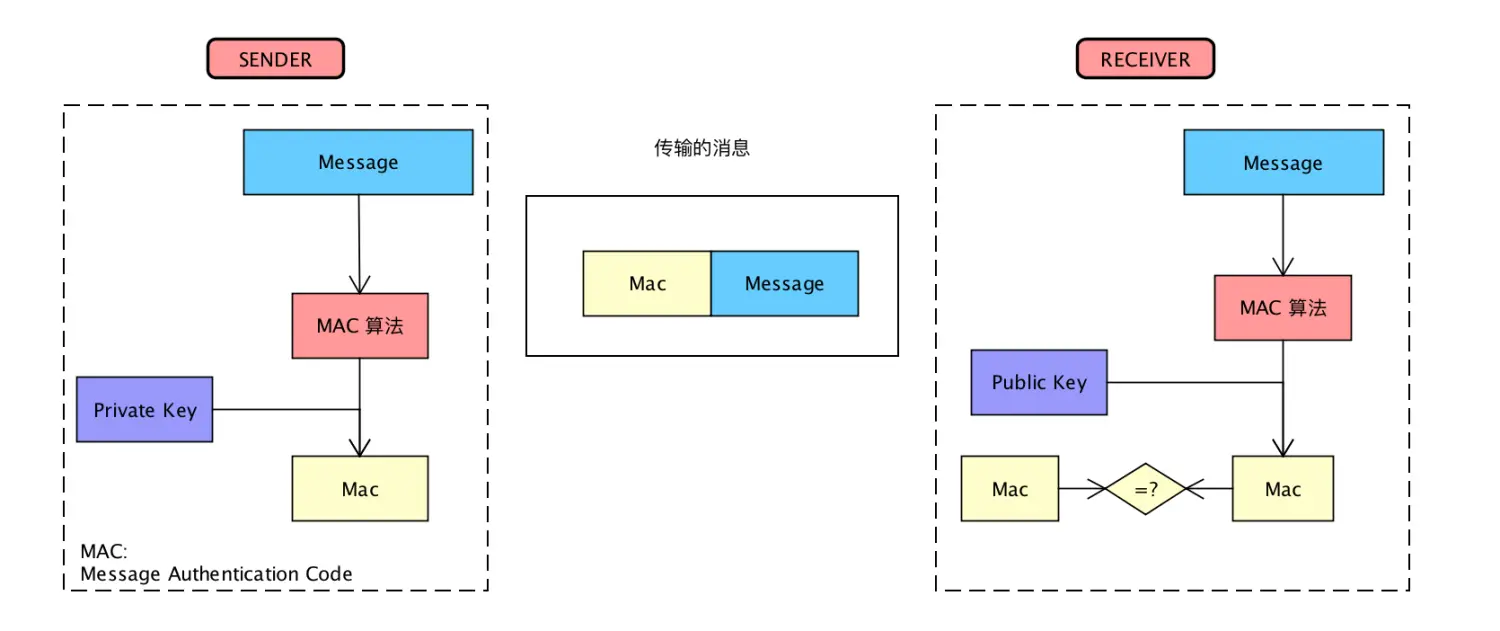
消息Message先通过MAC算法的散列函数生成摘要,然后用私钥签名生成签名Mac。验证时同样方法计算出Mac'和发来的Mac做对比
以太坊UDP加密流程
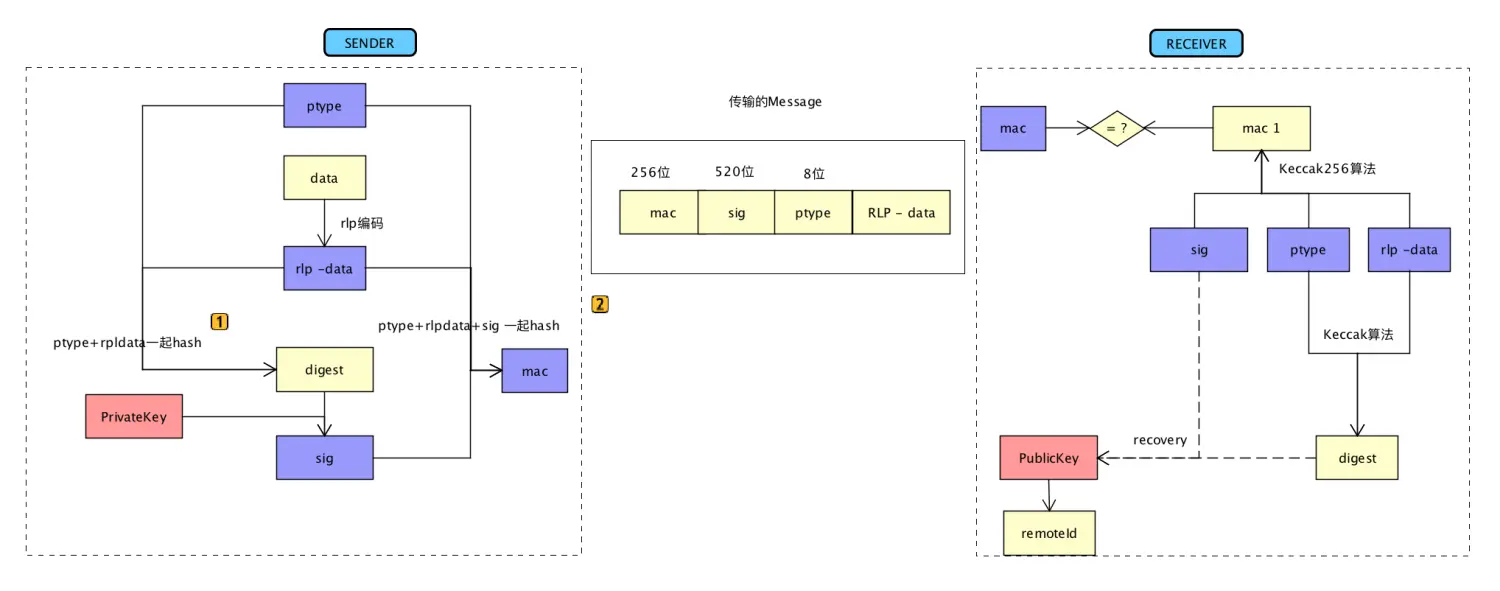
ptype是消息的事件类型,rlp-data是经过RLP编码后的数据,这两部分组成消息包的body。
digest为ptype和rlp-data的哈希值,私钥签名后得到sig,sig再和ptype、rlp-data一起哈希得到mac,mac和sig组成消息包的header。
验证时,将消息包中的sig、ptype、rlp-data哈希得到mac',与消息包的mac对比,确认是否没被篡改。ptype和rlp-data生成摘要digest',用digest'、sig、发送者公钥,验证消息包是否源自发送者。